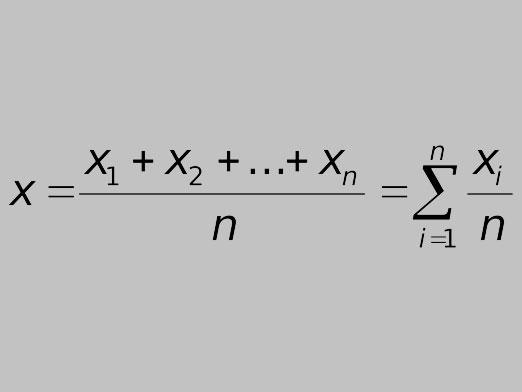Cum de a găsi o parabolă?

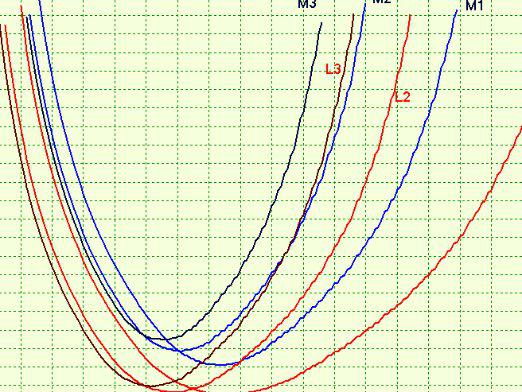
O parabolă este un grafic al unei funcții patrate. Această linie are un semnificație fizică semnificativă. Pentru a facilita găsirea vârfului unei parabole, trebuie să o desenați. Apoi, pe grafic puteți vedea cu ușurință partea sa de sus. Dar, pentru a construi o parabolă, este necesar să știm cum să găsim punctele unei parabole și cum să găsim coordonatele unei parabole.

Gasim punctele si varful parabolei

În reprezentarea generală, funcția patratică are următoarea formă: y = ax²+ bx + c. Graficul acestei ecuații este o parabolă. Dacă o> 0, sucursalele sale sunt direcționate în sus și pentru un <0 - în jos. Pentru a construi o parabolă pe un grafic, este necesar să cunoaștem trei puncte dacă trece pe axa ordinii. În caz contrar, ar trebui cunoscute patru puncte de construcție.

Atunci când găsim abscisa (x), este necesar să luăm coeficientul (x) din formula polinomică dată și apoi să împărțim de două ori coeficientul la (x²), apoi se înmulțește cu un număr - 1.

Pentru a găsi ordonata este necesar să găsim diferențiatul, apoi să îl înmulțim cu - 1, apoi să îl împărțim cu coeficientul la (x²), multiplicându-l mai întâi cu 4.

În plus, înlocuind valorile numerice, se calculeazăvârful unei parabole. Pentru toate calculele, este de dorit să folosiți un calculator de inginerie, iar atunci când desenați diagrame și parabole pentru a utiliza o riglă și un lumo-grafic, aceasta va crește semnificativ precizia calculelor.

Luați în considerare următorul exemplu, care ne va ajuta să înțelegem cum să găsim vârful unei parabole.

x²-9 = 0. În acest caz, coordonatele vârfului sunt calculate după cum urmează: punctul 1 (-0 / (2 * 1); punctul 2 - (0 ^ 2-4 * 1 * (-9)) / (4 * 1)). Astfel, coordonatele vârfului sunt valorile (0; 9).

Găsiți abscisa vârfului

După ce ați învățat cum să găsiți o parabolă și puteți calcula punctele de intersecție cu axa coordonatelor (x), puteți calcula cu ușurință abscisa vârfului.

Să presupunem că (x₁) și (x₂) sunt rădăcinile unei parabole. Rădăcinile parabolei sunt punctele de intersecție a acesteia cu axa abscisă. Aceste valori transformă la zero o ecuație cuadratoare cu următoarea formă: ax² + bx + c.

În acest caz | x₂| | > | x₁|, atunci vârful parabolei este situat în mijloc între ele. Astfel, el poate fi găsit prin următoarea expresie: x₀ = ½ (| x₂| | - | x₁|).

Găsiți zona figurinei

Pentru a găsi zona unei figuri pe o coordonatătrebuie să cunoașteți integralele. Și pentru ao aplica, este suficient să cunoaștem anumiți algoritmi. Pentru a găsi zona delimitată de parabole, este necesar să se producă imaginea într-un sistem de coordonate carteziene.

În primul rând, în conformitate cu metoda descrisă mai sus,coordonată a vârfului axei (x), apoi axa (y), după care se află vârful parabolei. Acum trebuie să determinăm limitele integrării. De regulă, acestea sunt indicate în starea problemei utilizând variabilele (a) și (b). Aceste valori trebuie plasate în partea superioară și inferioară a integralului, respectiv. Apoi, introduceți valoarea unei funcții într-o formă generală și multiplicați-o cu (dx). În cazul unei parabole: (x²) dx.

Apoi, trebuie să calculam într-o formă generală, antiderivativulvaloarea funcției. Pentru a face acest lucru, utilizați un tabel special de valori. Înlocuindu-se acolo limitele integrării, există o diferență. Această diferență va fi zona.

De exemplu, ia în considerare sistemul de ecuații: y = x₂+1 și x + y = 3.

Sunt abscise ale punctelor de intersecție: x₁= -2 și x₂= 1.

Presupunem că y₂= 3, în timp ce y₁= x² + 1, înlocuiți valorile din formula de mai sus și obțineți o valoare de 4,5.

Acum am învățat cum să găsim o parabolă și, pe baza acestor date, să calculeze zona figurinei, pe care o restrânge.