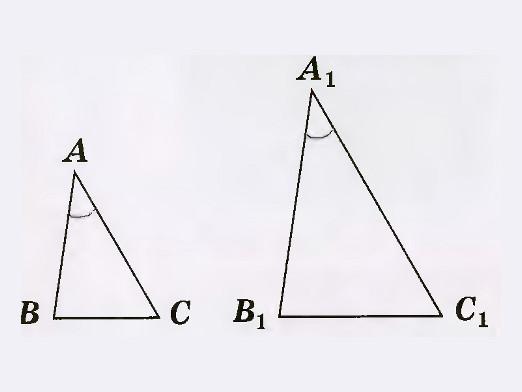
Semne de egalitate de triunghiuri

Toată lumea știe că două segmente vor fi egale dacălungimile lor coincid. Sau cercurile pot fi considerate egale dacă raza lor este egală. Și care sunt semnele de egalitate a triunghiurilor? Clasa a șasea a liceului: în lecția de geometrie, elevii învață că, se dovedește că există elemente pentru care egalitatea poate fi considerată egală cu triunghiurile care le conțin. Este foarte convenabil de utilizat în rezolvarea problemelor.
Primul semn al egalității de triunghiuri
Respectarea condiției de egalitate corespunzătoaredouă laturi și unghiul care este cuprins între ele într-un triunghi la două laturi și colțul care este închis între ele într-un alt triunghi, indică faptul că astfel de triunghiuri sunt egale.
Dovada.
Dacă luăm în considerare △ ABC și △ A1B1C1, unde laturile AB = A1B1, BC = B1C1,
și ∠ABC este egal cu ∠ A1B1C1,
atunci △ A1B1C1 poate fi suprapus pe △ ABC în așa fel încât ∠ A1B1C1 să coincidă cu ∠ABC. În acest caz, triunghiurile coincid complet, deoarece toate vârfurile lor coincid.
(Dacă este necesar, triunghiul A1B1C1 poate fi înlocuit cu un triunghi egal "inversat", adică un triunghi simetric cu A1B1C1.)
Al doilea semn al egalității de triunghiuri
Cu condiția ca o parte și două colțuri care suntsunt adiacent, respectiv lateral un triunghi și două colțuri, care sunt adiacenți în celălalt triunghi, aceste triunghiuri sunt considerate egale.
Dovada.
Dacă în △ ABC și △ A 1 B 1 C 1 sunt menținute următoarele egalități
AB = A1B1,
∠BAC = ∠B1A1C1,
∠ABC = ∠A1B1C1.
Suprapunem triunghiurile A1B1C1 și ABC unul pe celălaltastfel încât laturile egale AB și A1B1 și unghiurile care le învecinează coincid. Ca și în exemplul precedent, dacă este necesar, triunghiul A1B1C1 poate fi "întors și pus înapoi". Triunghiurile coincid și, prin urmare, pot fi considerate egale.
Al treilea semn al egalității de triunghiuri
Cu condiția ca cele trei laturi ale unui triunghi să fie egale cu cele trei laturi ale unui alt triunghi, atunci aceste triunghiuri sunt considerate egale. Dovada.
Să presupunem că pentru △ ABC și △ A1B1C1 egalitățileA1B1 = AB B1C1 = BC C1A1 = CA Deplasați triunghiul A1B1C1 astfel încât partea A1B1 să coincidă cu partea AB, iar vârfurile B1 și B, A1 și A să coincidă. Luăm un cerc cu centrul A și o rază de AC și un al doilea cerc cu centrul B și cu raza BC. Aceste cercuri se intersectează în două puncte simetrice în ceea ce privește segmentul AB: punctul C și punctul C2. Prin urmare, C1 după transferul triunghiului A1B1C1 trebuie să coincidă fie cu punctele C, fie cu C2. În orice caz, aceasta va însemna egalitatea △ ABC = △ A1B1C1, deoarece triunghiurile △ ABC = △ ABC2 sunt egale (de fapt aceste triunghiuri sunt simetrice în raport cu segmentul AB).
Semne de egalitate de triunghiuri de dreptunghiulare
În triunghiurile dreptunghiulare, unghiul dintre picioare este o linie dreaptă, deci în orice triunghi dreptunghiular există deja unghiuri egale. Prin urmare, următoarele observații sunt valide.
- Triunghiurile dreptunghiulare sunt egale dacă picioarele unuia dintre ele sunt egale cu picioarele celeilalte;
- Dreptunghiulare triunghiuri sunt egale, în cazul în care condiția de egalitate corespunzătoare a hypotenuse și unul din picioare în aceste triunghiuri este îndeplinită.
Dacă eliminăm din al doilea criteriu, care vorbește despre egalitatea triunghiurilor, condiția privind unghiul drept adiacent piciorului (deoarece unghiurile drepte în triunghiuri sunt egale), avem următoarele:
- astfel de triunghiuri sunt egale, cu condiția ca cateași, de asemenea, un unghi ascuțit adiacent acestuia într-un triunghi dreptunghiular, respectiv, sunt egale cu piciorul și unghiul ascuțit, într-un alt triunghi dreptunghiular.
Se știe că suma unghiurilor interioare ale unui triunghieste întotdeauna de 180˚, iar unul dintre unghiurile unui triunghi drept este o linie dreaptă. Prin urmare, dacă în două triunghiuri dreptunghiulare unghiurile ascuțite sunt egale, atunci unghiurile rămase sunt egale. Pentru triunghiurile obișnuite, non-dreptunghiulare, pentru a determina egalitatea cifrelor, este suficient să se știe că o parte și două colțuri sunt, respectiv, egale. Într-un triunghi în unghi drept, un singur unghi ascuțit și hypotenuse pot fi considerate pentru a determina egalitatea cifrelor.
- Dreptunghiulare triunghiuri vor fi egale cu condiția ca unghiul ascuțit și hypotenuse ale uneia dintre ele să fie egale cu unghiul ascuțit și hypotenuse în cealaltă.
Știință uimitoare - geometrie! Semne de egalitate de triunghiuri poate fi utilă nu numai pentru manualele școlare, dar, de asemenea, pentru rezolvarea sarcinilor de zi cu zi, care rezolva adulții din viața lor de zi cu zi.