Cum să găsiți laturile unui trapez?

Cursul de școală al geometriei implică cunoaștereacu tot felul de quadrangles, inclusiv trapezoidale. Cele mai de bază sarcini care se referă la trapezoizi sunt căutarea laturilor și captura. În acest articol, vom examina câteva exemple de rezolvare a problemelor privind găsirea laturilor unui trapez.

Trapezele sunt:

arbitrar;
isoscel;
dreptunghiular.

Rezolvarea problemelor pe un trapez arbitrar

Un trapez este un patrulater cu douălaturile sunt paralele, iar cele două nu sunt. Determinarea laturii într-un trapez arbitrar depinde de datele inițiale. Luați în considerare cazul în care sunt cunoscute unghiurile de la bază și de înălțime.

Sarcina 1

Se prezintă un trapez al ABCD, în care înălțimile VC și CM sunt egale cu 6 cm. Unghiurile de bază sunt de 60 și 45 de grade. Este necesar să găsiți laturile.

Deci, avem două triunghiuri în unghi drept AVKși SDM, care cunosc un picior și un colț opus. Cynos (raportul dintre piciorul opus și hypotenuse) pentru 60 și 45 de grade este cunoscut: sin 60 = √3 / 2, și sin 45 = √2 / 2.

Avem:

sin 60 = BK / AB, prin urmare AB = VK / sin 60
AB = 6 / √3 / 2 = 4,3 (cm)
sin 45 = CM / SD, deci SD = CM / sin 45
LED = 6 / √2 / 2 = 6√2 (cm)

Răspuns: AB = 4√3 cm și SD = 6√2 cm

Soluția problemelor pe un trapez dreptunghiular

Un dreptunghi este un trapez al cărui unghiuri la una dintre laturi sunt egale cu 90⁰. Luați în considerare un exemplu de cum să găsiți partea trapezoidală dacă celelalte trei laturi sunt cunoscute.

Problema 2. Sunt date trei laturi, dintre care unul este lateral perpendicular.

Să presupunem că avem un ABCD trapezoidală dreptunghiulară, în care AB este perpendicular pe BC. Se știe că AB = 12 cm, BC = 1 cm, AD = 6 cm. Este necesar să se găsească o latură mare laterală.

soluţie:

Din punctul C vom omite înălțimea SK și vom obține triunghiul dreptunghiular KDK și dreptunghiul ABCD. Deoarece părțile opuse ale dreptunghiului sunt CK = AB = 12 cm și AK = BC = 1 cm.

Gasim segmentul KD:

CD = AD - AK = 6 - 1 = 5 (cm)

Conform teoremei lui Pythagoras:

SD²= SK²+ CD²= 12²5²= 144 + 25 = 169
LED = √169 = 13 (cm)

Răspuns: LED = 13 cm

Problema 3. Având în vedere ambele baze și unghiul la bază

Având în vedere ABCD trapezoidală, în care bazele soarelui și tensiunea arterială sunt de 6 și respectiv 10 cm, unghiul VAD este drept, iar SDA este de 45 de grade. Găsiți partea mai mică.

Desenați înălțimea SC și obțineți un triunghi dreptunghiular SKD și un dreptunghi ABCS. Deoarece părțile opuse ale dreptunghiului sunt AK = BC = 6 cm.
CD = AD - AK = 10 - 6 = 4 cm
cos 45 = √2 / 2 = CD / LED, deci CD = CD / cos 45
Se obțin SD = 4 / √2 / 2 = 4√2 (cm)

Răspuns: SD = 4√2 cm

Rezolvarea problemelor unui trapez izoscel

Trapezoidul este numit izoscel, ale cărui laturi sunt egale. Pentru a înțelege cum să le găsiți, luați în considerare următoarele exemple

Problema 4. Ambele baze și înălțimi sunt date

Având o ABCD trapezoidală, în care AB = SD, și VC și CM - înălțimi. BC = 9 cm, AD = 19 cm, și BK = CM = 12 cm.

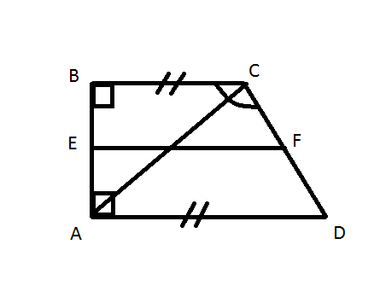
Să arătăm că triunghiurile ABK și DSM sunt egale. Prin starea AB = CD, VC = CM. Deoarece trapez isoscel, colțurile sunt VAK și SDM. Deoarece VC și cm înălțime, datele sunt triunghiuri dreptunghiulare. Prin urmare, AVC Unghi = 180 - (90 + HAC), iar unghiul DPA = 180 - (90 + SDM), precum și WAC și SDM sunt egale, atunci AVC și MSD prea. Astfel, triunghiurile ABK și DSM și DSM sunt egale pe ambele părți și unghiul dintre ele.

Se găsesc segmentele AK și MD.