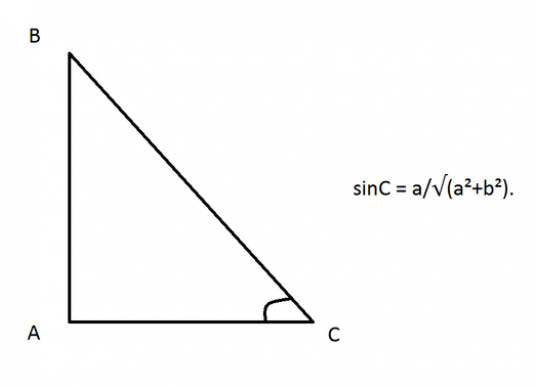Cum să găsiți sina colțului exterior?

Unghiile sinusoidale nu trebuie calculatedoar într-un triunghi drept, dar în oricare altul. Pentru a face acest lucru, este necesar să se deseneze înălțimea triunghiului (perpendicular pe una dintre laturi, coborât din colțul opus) și să rezolve problema ca și pentru un triunghi dreptunghiular, folosind ca unul dintre picioare înălțimea.
Cum să găsiți sina colțului exterior al unui triunghi
În primul rând trebuie să înțelegeți ce este un colț exterior. Avem un triunghi arbitrar ABC. Dacă una dintre laturi, de exemplu, AC, continuă dincolo de unghiul BAC și trage un fascicul AO, atunci noul unghi OAB va fi extern. Aici vom căuta sinusul lui.
Pentru a rezolva problema, trebuie să lăsăm BH perpendicular pe partea UA din unghiul ABC. Aceasta este înălțimea triunghiului. Cursul soluționării problemei va depinde de ceea ce știm.
Cea mai simplă opțiune este dacă știți unghiul TU. Apoi, problema este rezolvată foarte ușor. Deoarece raza OC este o linie dreaptă, unghiul OAC = 180 °. Prin urmare, unghiul OAB și BAC sunt adiacente, iar sinele unghiurilor adiacente sunt egale în magnitudine.
Să luăm în considerare o altă problemă: într-un triunghi arbitrar ABC este cunoscut lateral: AB = a și înălțimea BH = h. Este necesar să găsim sinele unghiului OAS. Din moment ce avem acum un triunghi dreptunghic AVN, AVN sinusul unghiului este egal cu raportul VN piciorul la ipotenuzei AB:
- sinBAH = BH / AB = h / a.
Acest lucru este de asemenea ușor. O problemă mai complicată, dacă înălțimea h este cunoscută și laturile AC = c, BC = b, este necesar să se găsească sinele unghiului OAB.
Prin teorema pitagoreană găsim cateterul CH al triunghiului VSN:
- BC2 = BH2 + CH2b2 = h2 + CH2,
- CH² = b² - h², CH = √ (b² - h²).
De aici puteți găsi un segment din partea AS a AC:
- AH = AC - CH = c - √ (b2 - h2).
Acum folosim din nou teorema lui Pythagorean pentru a găsi a treia parte a triunghiului AV ABN:
- AB² = BH² + AH² = h ² + (c - √ (b² - h²)) ².
Sinusul unghiului BAC este egal cu raportul dintre înălțimea VH a triunghiului și partea AB:
- sinBAC = BH / AH = h / (c - √ (b2 - h2)).
Deoarece unghiurile OAB și BAC sunt adiacente, sinusurile lor sunt egale în mărime.
Astfel, combinând teorema lui Pitagora, definițiasinus și alte teoreme (în special, pe unghiuri adiacente), este posibil să rezolvăm aproape majoritatea problemelor pe triunghiuri, inclusiv găsirea sinusului unghiului exterior. Uneori pot fi necesare construcții suplimentare: pentru a trage o înălțime de la unghiul dorit, pentru a continua partea laterală a unghiului dincolo de limitele sale și așa mai departe.