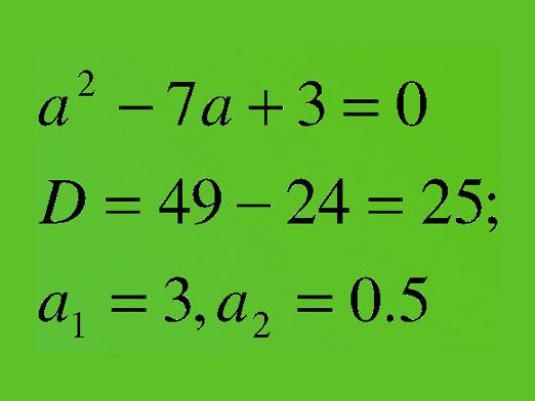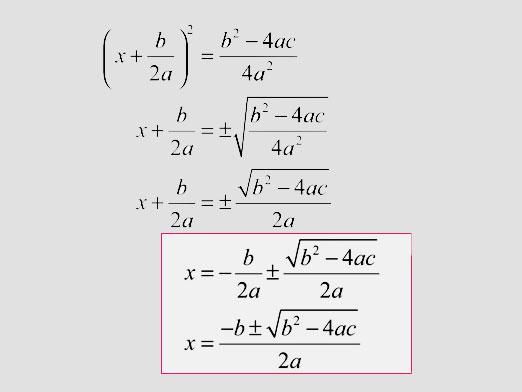Cum să găsiți rădăcina ecuației?

Una dintre secțiunile principale ale matematicii este o secțiune dedicată rezolvării ecuațiilor și găsirea rădăcinii ecuațiilor.

Înainte de a găsi rădăcina ecuației, mai întâi trebuie să dați seama ce este.

Rădăcina ecuației este valoarea necunoscutuluivalori în ecuația denotată cu litere latine (mai des - x, y, dar pot exista și alte litere). Acest lucru a fost menționat în articolul nostru - Care este rădăcina ecuației.

Luați în considerare cum să găsiți toate rădăcinile, pe diferite tipuri de ecuații și exemple specifice.

Ecuația formei ax + b = 0

Aceasta este o ecuație liniară cu o variabilă, unde a și b sunt numere, iar x este rădăcina ecuației.

Numărul rădăcinilor ecuației depinde de valorile a și b:

Dacă a = b = 0, atunci ecuația are un număr infinit de rădăcini.
Dacă a = 0, b nu este 0, atunci ecuația nu are rădăcini.
Dacă a nu este egală cu 0, atunci vom găsi rădăcina prin formula: x = - (b / a)

exemplu:

5x + 2 = 0
a = 5, b = 2
x = - (2/5)
x = -0,4

Răspuns: rădăcina ecuației este de 0,4

Ecuația este ax2 + bx + c = 0.

Aceasta este o ecuație patratică. Există câteva modalități de a găsi rădăcinile în ecuația patratică. Vom considera o soluție generală potrivită pentru rezolvarea oricăror valori ale lui a, b și c.

În primul rând, trebuie să găsim discriminantul (D) al acestei ecuații.

Pentru aceasta, există formula:

D = b²-4ac

În funcție de ceea ce a învățat discriminantul, există 3 opțiuni pentru soluții ulterioare:

Dacă D> 0, atunci rădăcinile lui 2. Și ele sunt calculate prin formule:
- x₁= (-b + √ D) / 2a.
- x₂= (-b - √ D) / 2a
Dacă D = 0, atunci rădăcina este una - se poate găsi prin formula: x = - (b / 2a)
Dacă D <0, atunci ecuația nu are rădăcini.

exemplu:

x²+ 3x-4 = 0

Aici a = 1, b = 3, c = -4

D = 3² - (4 * 1 * (- 4))
D = 9- (-16)
D = 9 + 16
D = 25

D> 0, atunci există 2 rădăcini în ecuație.

√D = √25 = 5

Înlocuiți toate valorile din formula noastră:

x₁ = (-3 + 5) / 2 * 1
x₁= 2/2
x₁= 1
x₂= (-3-5) / 2 * 1
x₂= (-8) / 2
x₂= -4

Răspuns: Rădăcinile ecuației sunt 1 și -4.

Ecuația formării toporului³+ bx²+ cx + d = 0

Aceasta este o ecuație cubică.

Există formule speciale ale matematicianului Cardano, din care se poate rezolva o astfel de ecuație, dar ele sunt foarte complexe. Vom merge pe celălalt, mai ușor de înțeles.

Ecuațiile cubice au întotdeauna cel puțin unarădăcină, iar valoarea sa este în mod tipic un număr întreg de la -3 la 3. Aceasta este, avem la dispoziție în ecuația va Inlocuitor pe rând, pentru x număr: -3, -2, -1, 0, 1, 2 și 3. Va fi X_1.

Este mult mai simplă și mai rapidă decât pare, și cu siguranță mai ușoară decât folosirea formulelor Cardano.

După ce găsim x₁, mergeți la căutare X₂ și X_3.

În acest scop, ne împărțim ecuația în (x-x₁) - acest lucru se poate face prin crearea parantezelor. Trebuie să avem o ecuație patratică, pe care am rezolvat-o puțin mai sus în acest articol.